Výběr analýzy
Každý uživatel si může libovolně zvolit, které z 5 analýz budou vypočteny pomocí zaškrtnutí jednotlivých políček pro: dosažitelnost, přitažlivost, spojitost, dále blízkost a přímost. Jednotlivé typy analýz jsou popsány níže.
Dosažitelnost (Reach)
Při výpočtu dosažitelnosti (Sevtsuk, 2010) je řešeno, kolik okolních budov spadá do stanoveného okruhu v prohledávané prostorové síti. Okruh dosažitelnosti Rr [i] budov i v diagramu G zjistí počet dalších budov v diagramu G, které jsou dosažitelné z bodu i na základě nejkratší vzdálenosti z maximálně stanoveného r.
Vztah je definován následovně:
kde d[i,j] je nejkratší vzdálenost mezi uzly i a j v diagramu G a |S| vyjadřuje mohutnost množiny S. Jestli, že dané uzly v diagramu G jsou vážené, pak je dosažitelnost definována na základě vztahu:
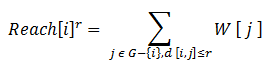
kde W [j] je váha uzlu j. V obrázku 6 je vykreslen způsob, jak je vypočítáván index dosažitelnosti. Obalové zóny jsou sledovány pro všechny budovy i a to v každém směru uliční sítě až po stanovený limitní poloměr r. Index dosažitelnosti odpovídá počtu míst (reprezentované menšími černými body), které se nacházejí v dosahu dané uliční sítě.
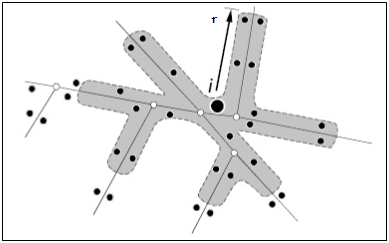
Dosažitelnost může být vypočtena na základě měření přístupu k jakémukoli místu. Aby se dalo co jednoduše vypočítat, kolik dalších budov spadá do daného okruhu stanoveného poloměru lze použít vyhledávací název atributu určitého uzlu, jehož váha může mít prázdné vstupní pole, tudíž ve výsledku bude vrácen pouze počet cílových budov spadajících do daného okruhu. Jako atribut však nemusí vždy být stanovená pouze velikost, uživatel může například stanovit atribut váhy jako objem daných budov (objem vyjádřen například jako počet lidí žijících v dané budově). V případě, že chceme zachytit dosažitelnost k určité činnosti, popřípadě k půdě, použijeme jako váhu atributu okolních budov například počet pracovních míst, počet obyvatel nebo obchodních zařízení.
Přitažlivostt (Gravity)
Vzhledem k tomu, že dosažitelnost se jednoduše spočítá, jako počet míst kolem každé budovy spadají do hledaného okruhu (volitelný atribut váhy). Míra přitažlivosti je navíc ovlivněna faktory prostorové impedance, která je potřebná k cestě do všech míst určení. Podle Hansena (1959), index přitažlivosti zůstává jednou z nejpopulárnějších prostorových opatření k usnadnění výzkumu dopravy. Při výpočtu přitažlivosti se předpokládá, že dostupnost budovy i je přímo úměrná přitažlivosti (váze) daného místa j v okolí i a nepřímo úměrná vzdálenosti mezi i a j:
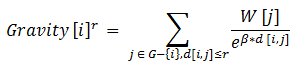
kde Gravity [i]r je index přitažlivosti k budově i v diagramu G v hledaném poloměru r (určen na základě pole vyhledávacího poloměru). W [j] je váha daného místa j, d[i,j] je geodetická vzdálenost mezi budovami i, j a β je exponent upravující vliv chyby (úpadku) z důvodu vzdálenosti. Index přitažlivosti zachycuje samotnou přitažlivost daného místa (W[j]), stejně jako prostorovou impedanci potřebnou k dosažení určitého místa (d[i,j]), kombinovanou s měřením dostupnosti. Pokud není dostupný žádný atribut váhy uzlu, pak je váha každé cílové budovy stanovena jako „1“.
Inverzní účinek dané vzdálenosti v indexu přitažlivosti klesá exponenciálně. Přesný tvar pro vzdálenost lze kontrolovat pomocí exponentu β, popřípadě pomocí vstupního pole níže. Exponent β a odpovídající tvar vzdálenosti by měly být stanoveny od předpokládaného způsobu cestování například – pro pěší měřené v „minutách“. V případě, že není zadán žádný vstup pro exponent β, pro vytvoření výstupu je automaticky použita hodnota „0“ a počítá se s předpokladem, že zde není žádná chyba (úpadek) ve vzdálenosti.
Spojitost (Betweennes)
Spojitost budovy je definována jako podíl nejkratší cesty mezi páry dalších budov v prostorové síti kolem dané budovy i. Je-li více než jedna možnost nejkratší cesty nacházející se mezi dvěma uzly, jak je tomu například v pravoúhlé struktuře (mřížce) ulic, pak každé z ekvidistantních (stejno délkových) cest je přidělena stejná váha tak, že se jedná o sumu vah jednotlivých. Výpočet spojitosti je definován takto:
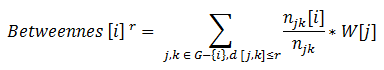
kde Betweennes [i]r je spojitost budovy i v hledaném okruhu o poloměru r (určen na základě pole vyhledávacího poloměru); njk[i] je počet nejkratších cest z uzlu j do uzlu k, které projdou budovou i; a njk je celkový počet nejkratších cest z uzlu j do uzlu k. Spojitost pro budovu i je vypočítávána na základě zvážení všech párů budov j,k které jsou v okruhu r od sebe. Nejedná se o výpočet, kde by došlo k výpočtu všech dvojic budov, které se nacházejí v okruhu o poloměru r od budovy i. A to především proto, že nepovažujeme za možné žádné cesty mezi budovami, které jsou delší než r od sebe. Pokud víme, že pár budov j,k je v rámci okruhu r od sebe a že nejkratší cesta z uzlu j do uzlu k (popřípadě z k do j) prochází budovou i, pak oba uzly j i k jsou taky do rozhodně do vzdálenosti okruhu r od budovy i.
Výpočet spojitosti se využívá především k odhadu potenciálu kolemjdoucích vzhledem k různým budovám v dané prostorové síti (využití například v demografii).
Blízkost (Closeness)
Blízkost vypočítávána ze vstupních budov, je definována jako inverzní funkce vzhledem k rostoucí vzdálenosti, která je potřebná k dosažitelnosti dané budovy od všech ostatních budov v dané síti, které spadají do okruhu stanoveného poloměru na základě nejkratší cesty (Sabidussi, 1966). Na základě výpočtu spojitosti můžeme stanovit potencionální provoz kolem dané budovy. Výpočet pro blízkost ukazuje na to, jak blízko jsou budovy od ostatních okolních budov na základě vzdálenostního prahu. V případě, že není k dispozici velikost prohledávaného okruhu, pak je index blízkosti vypočítáván pro všechny ostatní vstupní budovy v dané síti. Výpočet blízkosti je definován takto:
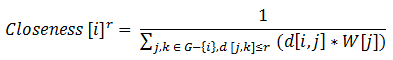
kde Closeness [i]r je spojitost budovy i v prohledávaném okruhu r (určen na základě pole vyhledávacího poloměru), d[i,j] je nejkratší vzdálenost mezi uzly i a j a W[j] je váha cílové budovy j.
Přímost (Straightness)
Metrika přímosti (Vragovic, Louis, et al., 2005) vyjadřuje, do jaké míry dané nejkratší cesty z uzlu zájmu do všech ostatních uzlů připomínají euklidovské cesty. Jinak řečeno, metrika přímosti zachycuje kladné odchylky v cestovní vzdálenosti, které vyplývají z proporcí dané uliční sítě oproti lineární vzdálenosti na beztvaré rovině. Přímost je formálně definována (Porta, Crucitti et al., 2005) jako:
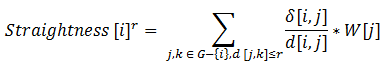
kde Straightness [i]r je přímost budovy i v stanoveném okruhu r, δ[i,j] je euklidovská vzdálenost mezi budovami i a j, d[i,j] je nejkratší síťová (uliční) vzdálenost mezi stejnými budovami. Index přímosti v podstatě vyjadřuje jak dlouhé je cestovní spojení z každé budovy na okolní body j. Tudíž je důležité si uvědomit, že index přímosti by měl být použit pouze v případě, že je atribut impedance v podobě lineární vzdálenosti.
Bakalářská práce
Autor: Jakub Vrkoč
Vedoucí práce:
RNDr. Jaroslav Burian, Ph.D

 Univerzita Palackého v Olomouci
Univerzita Palackého v Olomouci
Bakalářská práce ke stažení