Zhodnocení dostupných technik sběru dat pro konstrukci
podélného profilu vodního toku
Jan MARTÍNEK, vedoucí práce: RNDr. Michal Bíl, Ph.D.
5. VÝSLEDKY PRÁCE
5.1. Výsledky z měření totální stanicí
Nejpřesnější metodou měření je bezesporu měření za pomoci totální stanice, na což ostatně poukazují i výsledky z terénního sběru dat uskutečněném na tocích Javoříčce a Vráženském potoce, které jsou uvedeny v tabulkách Tab.1. a Tab.2. V nich jsou zapsány jednak výškové hodnoty obdržené z měření za pomoci totální stanice (v terénu byly zaměřeny kontrolní orientace na body o známých souřadnicích) a jednak také skutečné výškové hodnoty, jenž byly získány z databáze trigonometrických a zhušťovacích bodů. Z rozdílů těchto hodnot lze potom získat informaci o velikosti chyb vzniklých nepřesným měřením. Na obou VT byly takto zaměřeny tři kontrolní orientace, a to na Javoříčce body ZHB0211, ZHB0214 a ZHB0215 a na Vráženském potoku body TB0035, ZHB0244, ZHB0245. Jak lze vidět, maximální chyba byla zaznamenána na bodu č. TB0035 v blízkosti Vráženského potoka o velikosti 18 cm. Z jednoduchého statistickém vyhodnocení bylo dále zjištěno, že na VT Javoříčce je průměrná chyba 0,06 m a maximální chyba 0,11 m, zatímco na Vráženském potoce průměrná chyba činí 0,1 m a maximální chyba 0,18 m. V celkovém hodnocení jsou tedy měření na VT Javoříčce více přesná než na Vráženském potoku, což koreluje s náročností měření odvíjející se od členitosti reliéfu a od rozložení vegetace.
| ID bodu | naměřená výška [m] | skutečná výška (dle DATAZ) [m] | rozdíl výšek (chyba) [m] |
|---|---|---|---|
| ZHB0211 | 401,58 | 401,47 | 0,11 |
| ZHB0214 | 436,72 | 436,77 | 0,05 |
| ZHB0215 | 478,78 | 478,75 | 0,03 |
| ID bodu | naměřená výška [m] | skutečná výška (dle DATAZ) [m] | rozdíl výšek (chyba) [m] |
|---|---|---|---|
| TB0035 | 344,54 | 344,72 | 0,18 |
| ZHB0244 | 372,48 | 372,44 | 0,04 |
| ZHB0245 | 348,53 | 348,45 | 0,08 |
5.2. Výsledky z měření metodou RTK
V případě volného výhledu na oblohu je nejlepší volbou jistě metoda RTK. Je rychlá, přesná a nenáročná na počty pracovníků. Co se týče ceny, je otázkou, zda-li je opravdu nutné investovat do drahých GPS přijímačů. Pokud se podíváme na hodnoty uvedené v tabulce Tab.3., můžeme vidět, že velice dobrých výsledků dosahují i přístroje v mnohem nižší cenové kategorii. Když navíc vezmeme v potaz, že pro postprocesní zpracování byla v programu PPro2Static vybrána pouze nejméně přesná metoda DGPS CODE, můžeme konstatovat, že jsou výsledky z měření více než dobré. V případě použití metody L1 Fixed, která je však dostupná pouze v komerční verzi tohoto softwaru, by bylo potom možné dosáhnou až centimetrové přesnosti, což je již na úrovni dnes nejpřesnější DGPS přístrojů. Jestliže bychom tedy zakoupili GPS přístroj v hodnotě cca 8000 Kč, PDA v hodnotě přibližně 10000 Kč, další potřebné příslušenství (externí napájení, kabely apod.) v hodnotě 3000 Kč a komerční verzi postprcesního softwaru PPro2Static za cenu 15000 Kč, získáme tak plnohodnotný GPS RTK systém s centimetrovou přesností v celkové hodnotě cca 36000 Kč.
| Přesnost Y(Š) [m] | Přesnost X(D) [m] | Přesnost Z [m] | Doba měření [min] |
|---|---|---|---|
| -0,12 | 0,29 | 0,371 | 15 |
| -0,48 | -0,05 | 0,112 | 4 |
| -0,07 | 0,41 | 0,227 | 4 |
| 0,09 | 0,17 | 0,851 | 4 |
| -0,06 | 0,29 | 0,495 | 4 |
| 0,06 | 0,7 | 0,348 | 4 |
| -0,07 | 0,37 | 0,344 | 4 |
| -0,29 | 0,24 | 0,233 | 4 |
| -0,15 | 0,21 | 0,632 | 3 |
| -0,23 | 0,16 | 0,772 | 2 |
| -0,46 | 0,17 | 1,399 | 1 |
5.3. Výsledky z měření GPS metodou a barometrickým výškoměrem
Samotná měření byla provedena jednak klasickou metodou GPS (u přístrojů Navilock, Evolve a Antaris) a jednak také s pomocí barometrického výškoměru (v případě přijímače GARMIN). Pro jednotlivé techniky měření byla vždy vypočítána průměrná a maximální odchylka od skutečné hodnoty získané z měření totální stanicí, dále byly zjištěny maximální odchylky od skutečné hodnoty v souboru 50%, 90% a 95% vybraných bodů na VT. Hodnocení bylo provedeno jak pro neopravené výškové hodnoty, tak i pro výšky přepočítané jednou z opravných funkcí. Část výsledků z tohoto statistického hodnocení lze vidět v tabulkách Tab.4 a Tab.5.
Na základě analýzy prezentovaných hodnot je možné říci, že nejpřesnějších výsledků dosahuje v kategorii klasických GPS přístrojů přijímač ANTARIS s chipsetem LEA-4T (UBX), těsně za ním následuje přístroj Navilock s chipsetem Sirf III a jako poslední se umístil přístroj Evolve s chipsetem MTK. Je však potřeba zmínit, že toto hodnocení řeší pouze výškovou přesnost. Pokud by se hodnotila přesnost i v poloze, je možné, že budou výsledky poněkud jiné (zejména pak mezi přijímači s chipsetem MTK a Sirf III).
Co se týče barometrického výškoměru obsaženého v GPS přijímači GARMIN, zde je možné hovořit o srovnatelných výsledcích jako v případě přístroje ANTARIS. Pokud by však byly hodnoty postprocesně ještě dále zpracovány, bylo by dosaženo jednoznačně lepších výsledků než u GPSky od švýcarské firmy u-Blox.
| 50% [m] | 90% [m] | 95% [m] | PRUM [m] | MAX [m] | |
|---|---|---|---|---|---|
| UBX | 4,625 | 13,827 | 17,047 | 6,411 | 48,093 |
| MTK | 7,6 | 27,738 | 36,691 | 11,445 | 66,945 |
| SIRF | 5,612 | 22,655 | 33,383 | 9,935 | 88,179 |
| GAR | 5,639 | 12,796 | 15,345 | 6,054 | 17,974 |
| 50% [m] | 90% [m] | 95% [m] | PRUM [m] | MAX [m] | |
|---|---|---|---|---|---|
| UBX | 4,056 | 12,012 | 15,918 | 5,528 | 47,743 |
| MTK | 7,683 | 24,437 | 32,025 | 10,272 | 44,779 |
| SIRF | 3,72 | 13,127 | 21,737 | 6,285 | 65,044 |
| GAR | 1,672 | 4,276 | 5,266 | 2,053 | 9,587 |
V případě analytického zpracování jednotlivých výstupů z GPS měření bylo kromě hodnocení přesnosti měření prováděno také studium vztahů mezi velikostí chyb z měření a podmínkami, ve kterých měření probíhalo, jako jsou výška vegetace a výška horizontu. Jak lze vidět na grafech Obr.19 až Obr.22 obsažených v příloze č. 2, přesnost měření úzce souvisí zejména s výškou vegetace. Čím je vegetace vyšší, tím je i větší chyba. Tato korelace je patrná zvláště u Vráženského potoka (Obr.21 a Obr.22 v příloze č.2). Ačkoli by se mohlo zdát, že podobný vztah bude i u výšky horizontu, korelace v tomto případě nebyla prokázána (viz Obr.23 až Obr.26 v příloze č.2). Co je však zajímavé, existují zde jisté souvislosti mezi spádem svahů nacházejících se poblíž VT a velikostí chyby měření. Čím jsou okolní svahy prudší, tím je chyba vyšší. Z toho lze usuzovat, že se chyby během měření zvětšují ani ne tak vlivem vyšší výšky horizontu (a tím i omezeného výhledu na jednotlivé satelity) jako spíš následkem intenzivnějšího vícecestného šíření vln odrážejících se od prudších svahů a kmenů stromů, nacházejících se v mnohem větší úhlové výšce než za obvyklých podmínek.
5.4. Výsledky z upravených sekundárních dat
Jak lze vidět v tabulce Tab.6, u sekundárních dat bylo dosaženo nejpřesnějších výsledků u ZABAGEDu potažmo Základní mapy ČR 1:10 000. Aby však bylo dosaženo takovéto přesnosti, je nutné se přesně držet zásad uvedených v této práci. Jednak je potřeba důkladně překontrolovat vektorová data ZABAGEDu, zda-li sedí s daty ZM10, jednak je také nutné doplnit všechny chybějící výškové hodnoty, které byly z mapy vypuštěny z důvodu výskytu srázů či jiných výraznějších překážek. Pokud takto data opravíme, můžeme dosáhnout až metrové přesnosti. Přestože je přesnost v případě DMU25 již o poznání horší, pro měřítko 1:25000, ve kterém je tento model vykreslen, je více než dostačující.
| 50% [m] | 90% [m] | 95% [m] | PRUM [m] | MAX [m] | |
|---|---|---|---|---|---|
| ZM10 | 0,642 | 1,598 | 2,054 | 0,801 | 3,757 |
| DMU | 1,932 | 6,064 | 8,916 | 2,712 | 15,332 |
5.5. Celkové hodnocení
V rámci celkového hodnocení byly sledovány tyto faktory: doba potřebná k zaměření 1 km vodního toku, minimální počet pracovníků nutný k uskutečnění měření, dále přesnost měření před opravou a po opravě u 95% z celkového množství zaměřených bodů (komplexní přehled přesností výškových hodnot je graficky znázorněn na obrázku Obr.2) a konečně také výše finančních nákladů, které v sobě zahrnují jak cenu přístroje, tak také cenu veškerého příslušenství. Pro přehlednost byly výsledky z hodnocení vloženy do přehledné tabulky (viz Tab.8), která je vlastně hlavním výsledkem této práce.
Kromě číselného vyjádření jsou některé části tabulky (konkrétně sloupce udávající přesnost u 95% studovaných bodů) také barevně rozlišeny a to podle toho, pro jaké vertikální měřítko jsou výsledky z jednotlivých technik sběru dat vhodné. Pod pojmem vertikální měřítko je v tomto případě myšleno rozlišení na vertikální ose Y, tedy stupeň rozlišení ve výšce. Čím je měřítko větší, tím jsou samozřejmě větší také nároky na přesnost dat.. Aby mohla být data vizualizována v příslušném měřítku, musí být vždy zachována podmínka:
VELIKOST CHYBY : VELIKOST MĚŘÍTKA ≤ 1 MM
Pokud by tato podmínka nebyla dodržena, chyba by na vykresleném profilu byla již viditelná, což by bylo samozřejmě špatně. Jestliže je tedy velikost chyby např. 20 metrů (počítáme s 95% chybou), pak lze použít maximálně měřítko 1:20 000. V této práci bylo provedeno rozřazení do celkem 6 různých měřítek. Jejich hodnoty a k nim přidělené barvy jsou zobrazeny v tabulce Tab.7.
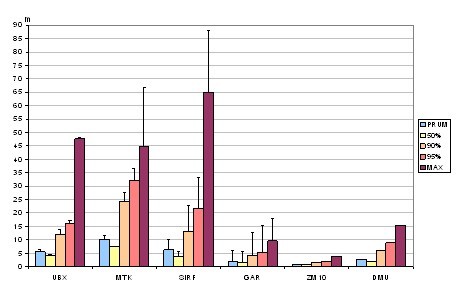
Obr.2.: Statistické vyhodnocení přesnosti výškových hodnot u obou toků
po opravě pro jednotlivé techniky sběru dat; rozdíl mezi velkostí chyby před
opravou a po opravě (po zpřesnění průběhu podélného profilu) je v grafu
vyjádřen chybovou úsečkou
| ..................... 1 : 200 ..................... |
| ..................... 1 : 1 000 ................... |
| ..................... 1 : 5 000 ................... |
| ..................... 1 : 10 000 .................. |
| ..................... 1 : 20 000 .................. |
| ..................... 1 : 50 000 .................. |
| Doba měření na 1km [hod] | Počet prac. | Přesnost měření bez opravy u 95% bodů [m] | Přesnost měření po opravě u 95% bodů [m] | Náklady [Kč] | |
|---|---|---|---|---|---|
| Totální stanice | 16,0 | 2 | 0,2 | 0,2 | 150 000,- |
| u-Blox | 0,5 | 1 | 17,0 | 15,9 | 15 000,- |
| MTK-Evolve | 0,5 | 1 | 36,7 | 32,1 | 7 000,- |
| SIRF-Navilock | 0,5 | 1 | 33,4 | 21,7 | 7 000,- |
| GARMIN | 0,5 | 1 | 15,3 | 5,3 | 15 000,- |
| ProMark2 | 1,5 | 1 | - | - | 100 000,- |
| DIGIT. SKLON | 4,0 | 1 | - | - | 35 000,- |
| ZABAGED | - | - | - | 2,1 | 1ML 1000,- |
| DMU | - | - | 8,9 | 8,9 | NEPRODEJNÉ |