Případová studie
Využití modelu GLMM pro hodnocení navigace OLINA
Dada pro tuto případovou studii pochází z dotazníků, díky nimž bylo zjištěno, jak vybraní lidé vnímají navigaci OLINA, turistický multimediální průvodce Olomoucí. Dotazníky byly vyplněny v roce 2011 a 2012 stejnými subjekty v rámci projektu OLINA.
Data a jejich zpracování
DJak již bylo řečeno, data byla sbírána za účelem hodnocení turistického multimediálního průvodce Olomoucí - OLINA. Tento průvodce umožňuje přístup k tisícům fotografií, hodiny audiovizuálních záznamů a nesčetně psaných komentářů o městě Olomouc. Na zpracování projektu OLINA se podílela česká firma Digital Urban Legends, město Olomouc a Katedra geoinformatiky, Univerzity Palackého v Olomouci. Více informací na http://geoinformatics.upol.cz/olina/.
OT1 - Hodnocení ovladatelnosti a srozumitelnosti Turistického multimediálního průvodce Olomoucí - OLINA (1 - Nejlepší, 5 - Nejhorší)
OT2 - Hodnocení grafického zpracování a doprovodného grafického materiálu Turistického multimediálního průvodce Olomoucí - OLINA (1 - Nejlepší, 5 - Nejhorší)
OT3 - Hodnocení textového zpracování pro body zájmu a reálie Turistického multimediálního průvodce Olomoucí - OLINA (1 - Nejlepší, 5 - Nejhorší)
OT4 - Hodnocení atraktivity zvolených tras Turistického multimediálního průvodce Olomoucí - OLINA (1 - Nejlepší, 5 - Nejhorší)
OT5 - Celkové hodnocení Turistického multimediálního průvodce OLINA v Olomouci (1 - Nejlepší, 5 - Nejhorší)
## načtení dat, o jako olina
o <- read.delim("D:/dat_olina.txt")
## zda jsou faktory
str(o)
## převod proměnných na faktory
o$ID < factor(o$ID)
## snížení počtu proměnných
summary(aov(o$OT5~o$OT1*o$OT2*o$OT3*o$OT4))
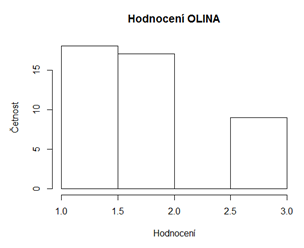
hist(o$OT5, main = paste("Hodnocení OLINA"), xlab="Hodnocení", ylab="Četnost" )
Snížení faktorů pomocí GLM a tvorba modelu GLMM
## vytvoření GLM, pozor na hodnotu family, zde je poissonovo rozdělení
o.glm1<glm(formula = OT5 ~ OT1 + OT2 + OT3 + OT4, family = poisson(identity), data = o)
## výpočet stepwise regrese
stepwise(GLM.4, direction='backward/forward', criterion='BIC')
## vytvoření GLMM modelu, do modelu lmer není nutné zadávat family, pozná, ## že je poissonovo rozdělení
o.lmer1<lmer(o$OT5~1+o$rok+(1+o$rok|o$ID)+(1|o$OT2),data=o)
Zda byl vybrán dobrý model, lze zjistit jednoduše. Bude porovnán se složitějším. Pomocí stepwise regrese, zjistíme, že druhý nejlepší model v sobě počítá i s OT3. Proto vytvoříme model o.lmer2 a porovnáme oba modely pomocí anovy.
o.lmer2<lmer(o$OT5~1+o$rok+(1+o$rok|o$ID)+(1|o$OT2)+(1|o$OT3),family="poisson",data=o, REML=0)

Nulová vypotéza je model o.lmer1 a alternativní hypotéza je o.lmer2. Díky velkému p-value, nelze zamítnout nulovou hypotézu ve prospěch alternativní. Proto se preferuje model o.lmer1.
Zda byl vybrán dobrý model, lze zjistit jednoduše. Bude porovnán se složitějším. Pomocí stepwise regrese, zjistíme, že druhý nejlepší model v sobě počítá i s OT3. Proto vytvoříme model o.lmer2 a porovnáme oba modely pomocí anovy.
o.lmer2<lmer(o$OT5~1+o$rok+(1+o$rok|o$ID)+(1|o$OT2)+(1|o$OT3),family="poisson",data=o, REML=0)

Nulová vypotéza je model o.lmer1 a alternativní hypotéza je o.lmer2. Díky velkému p-value, nelze zamítnout nulovou hypotézu ve prospěch alternativní. Proto se preferuje model o.lmer1.
Výsledky
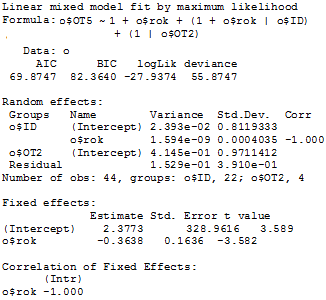
Variance jsou obecně velmi malé, v řádech deseti na mínus první až devátou. Počáteční průměrná hodnota Interceptu je 2.3773, tedy průměrné celkové počáteční ohodnocení OLINY. I když je sklon za roky záporný (-0.3638), tak dobré mínění o turistickém průvodci roste. To je způsobeno inverzní stupnicí. Sklon v letech u náhodného efektu je 0.0004035, tedy téměř žádný. Výsledná rovnice je ve tvaru:
OT5=0.8119333*ID+0.9711412*OT2+ 0.0004035*rok+2.3773+(-0.3638)
Ze směrodatné odchylky náhodných efektů ID a OT2, které jsou si celkem podobné, se dá odhadnout spodní a horní hranice celkového ohodnocení OLINY. Tedy rozpětí je přibližně ±1. Horní hranice, tedy nejlepší známka, kterou se OLINA ohodnotila je 1. Spodní hranice, tedy nejhorší známka, kterou se OLINA ohodnotila je 3.
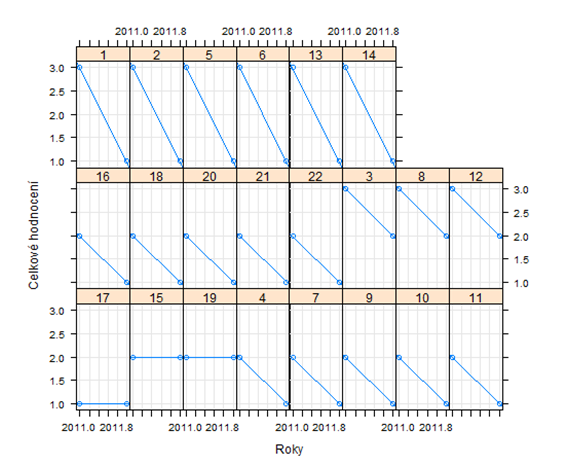
Ze sklonů náhodných (0.0004035) a neměnných (-0.3638) efektů pro roky lze také vypočítat hraniční intervaly sklonu. Pro Výpočet je následovný: 0-2*(-0.36)=0.72 ohodnocení OLINY/roky (spodní hranice) a 0+2*(-0.36)=-0,72 ohodnocení/roky (horní hranice). To znamená, že se sklon pohyboval v ± 0,72. Ale z grafu 4 vidíme, že některé subjekty se vymykají těmto intervalům, to je ovšem správně. Tyto intervaly jsou počítané od průměrné hodnoty.
Korelace dosahuje extrémní hodnoty -1. To je zapříčiněno tím, že celkové ohodnocení OLINY, bylo povětšinou stejné jako ohodnocení otázky 2 (Hodnocení grafického zpracování a doprovodného grafického materiálu Turistického multimediálního průvodce Olomoucí - OLINA). Z toho tedy plyne, že celkové ohodnocení, bylo podmíněno grafickým zpracováním OLINY a ostatní atributy byly pro celkové hodnocení málo podstatné.
## hodnocení během let
print(dotplot(reorder(o$rok, o$OT5) ~ o$OT5, a,ylab = "Rok", jitter.y = TRUE, pch = 21,xlab = "Celkové hodnocení",type = c("p", "a")))
## míra a prudkost změny subjektů
print(xyplot(o$OT5 ~ o$rok| o$ID, o, aspect = "xy",layout = c(8,3), type = c("g", "p", "r"),index.cond = function(x,y) coef(lm(y ~ x))[1],xlab = "Roky",ylab = "Celkové hodnocení"))
Diskuze
Datová sada, je velmi jednoduchá proto, aby se upevnily nabité znalosti z teoretického bloku. A také byla použita subjektivní data.
Položené otázky v dotazníku jsou dobře sestaveny a i stupnice ohodnocení je přirozená. Jen bylo naměřeno málo subjektů.
Proto byla použita pro upevnění modelu metoda maximální pravděpodobnosti, která je právě pro tyto případy vhodnější, to potvrdila i anova. I když by měla mít tato metoda, v nejideálnějším případě, data s gaussovým rozdělením poissonovo rozdělení zvládne také.