Longitudinální data
Longitudinální data
Longitudinální data v sobě obsahují informaci o časové následnosti. Pozorované proměnné jsou naměřeny v průběhu určitého časového intervalu, tedy jsou opakovatelně měřeny za daný čas. Pozorované proměnné jsou vždy tytéž nebo jsou z velmi podobné skupiny (př. zkoumám 10 humrů, které mám v akváriu, jak rostou za 5 let, či zkoumám růst populace humrů za 5 let ve volné přírodě, když pokaždé vylovím jiného jedince). Ohrožení lesních porostů z hlediska výskytu větrných polomů je objektivně provádět s pomocí modelů a klasifikací, či vlastním (subjektivním) pozorováním přímo v terénu. Nejjednodušší vymezené postupů k hodnocení rizika polomů je přístup empirický, mechanický a přístup založený na pozorování.
Longitudinální analýza dokáže charakterizovat časový trend v rámci subjektů a mezi subjekty. V datech se vždy bude nacházet odezva, jakou měl subjekt v době pozorování určitého měřeného faktoru. Je možno také analyzovat vztah mezi testovacími a kontrolními subjekty, vztah v rámci subjektů či mezi subjekty. To už bylo nastíněno u datové sady InstEval, kde studenti ohodnocovali své učitele v průběhu let své školní docházky.
Příklad:
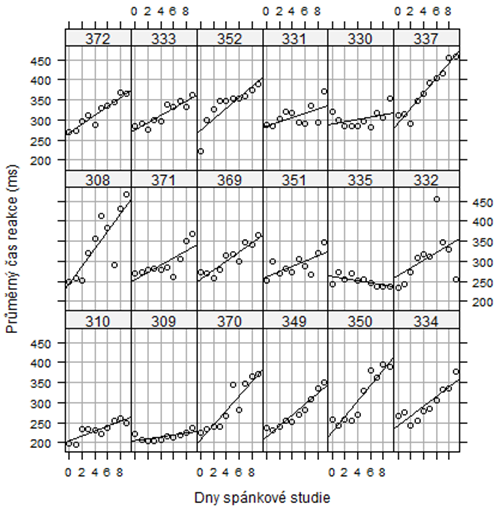
Jako ukázkový příklad byla vybrána studie o spánkových návycích řidičů kamiónů jménem „SleepStudy“, data v balíku lme4. Subjekty, tedy vybraní řidiči, byli rozděleni do skupin, ve kterých řidiči mohli spát jen po omezenou dobu. Zde je analyzována skupina 18 subjektů, kterým bylo dovoleno spát jen tři hodiny denně a pak se jim několikrát změřil reakční čas. Data obsahují 180 pozorování a 3 proměnné: Reakce (Reaction, změřená doba reakce, v každém z deseti dnů), Dny (Days, počet po sobě následujících dnů, tedy 10 dnů) a Subjekt (Subject, 18 zkoumaných řidičů, kteří byli 10 krát měřeni, tedy každý den jednou).

print(xyplot(Reaction ~ Days | Subject, sleepstudy, aspect = "xy",layout = c(6,3), type = c("g", "p", "r"),index.cond = function(x,y) coef(lm(y ~ x))[1],xlab = "Dny spánkové studie",ylab = "Průměrný čas reakce (ms)"))
Pro uchycení modelu se použijí dva neměnné parametry, a to Intercept a sklon regresní přímky pro časový trend, a dva náhodné parametry pro Subjekt. Náhodné efekty pro daný Subjekt jsou rozdíly v Interceptu a sklonu časového trendu pro populaci. Sklon je typická změna Reakce Subjektu v čase spánkové studie a je vyjádřen regresní přímkou. Intercept je průměrná doba Reakce Subjektu v jednotlivých dnech. Náhodný efekt pro daný Subjekt je odchylka v Interceptu a sklonu časového trendu pro Subjekt. Budou vytvořeny dva modely.
Výsledek:
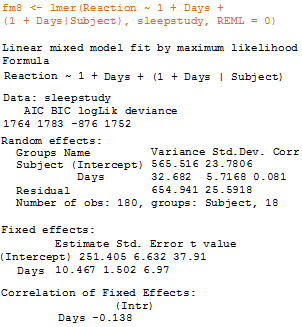
Výsledek korelace, který je blízko extrémních hodnot <-1; 1> vypovídá o tom, že model nemůže být dobře zformulovaný. Zde je hodnota korelace malá, 0,081, proto můžeme říci, že model může být dobrý.
Odhady parametrů pro neměnné efekty jsou 251,405 (Intercept) a 10,467 (Dny). Tyto hodnoty představují typickou počáteční reakční dobu řidičů bez spánkového deficitu (cca 250 milisekund) a typický vzrůst (sklon) reakční doby řidičů (tedy cca10,5 milisekund za každý den spánkového deficitu). V náhodných efektech je sklon vyjádřen číslem 5.7168, což je asi 6ms za dny.
Odhadnutá směrodatná odchylka pro Subjekt ku Subjektu v Interceptu je 23,7806, to koresponduje se směrodatnou odchylkou Residual, 25,5918 ms. Tyto hodnoty vyjadřují, jak se od sebe jednotlivé Subjekty liší. Odhad intervalu pro 95% by měly být okolo ±50ms. Po kombinaci těchto rozsahů s celkovou průměrnou reakční dobou (250 ms) budou hodnoty Intercepty v intervalu od 200ms do 300ms.
Ze sklonů náhodných (5.7168) a neměnných (10.467) efektů pro Dny lze také vypočítat hraniční intervaly sklonu. Výpočet je následovný: 10.5-2*5,7=−0.9 ms/Dny (spodní hranice) a
10,5+2*5,7=21.9 ms/Dny (horní hranice).
Odhady korelace v rámci Subjektů pro náhodné efekty a sklony jsou velmi nízké, 0,081. Což ukazuje na to, že jsou nedostatek spánku a délka reakční doby v určitém vztahu. Ale už nemůžeme říci, zda nedostatek spánku opravdu tak silně ovlivňuje pozorované počáteční reakční doby Subjektů. Takový malý korelační koeficient také naznačuje, že můžeme získat dobré umístění modelu i bez korelace.
Model s korelovanými náhodnými efekty
První model dovolí korelaci náhodných efektů pro stejný Subjekt (nepodmíněná distribuce). To například znamená, že Subjekty s delší počáteční reakční dobou mohou být silněji ovlivněni nedostatkem spánku. Druhý model zaručí nezávislost náhodných efektů pro Intercept a sklon každého Subjektu.
Korelace vyjadřuje vzájemný lineární vztah dvou proměnných. Pokud se jedna proměnná mění, mění se i jejich vztah. Pokud vykazují dvě proměnné vzájemnou korelaci, tak je jedna proměnná označována jako příčina a druhá jako následek. Výsledek korelace, tedy její míra, je v intervalu od <-1;1>.
Model s nezávislými náhodnými efekty
Pro modely s jednoduchým skalárními náhodnými efekty, kde bylo třeba vyjádřit jejich seskupení, byla použita formule (1|faktor). Ve spánkovou studii je jeden jednoduchý náhodný efekt pro Subjekt, (1|Subject).
Protože Subjekty závisí na Dnech, tak je třeba vytvořit další seskupující parametr. Ten lze zapsat jako (0+Days|Subject). V tomto zápisu budou náhodné efekty sami produkovat korelovaný vektor hodnot náhodných efektů. Nula v zápisu znamená žádný Intercept a zápis Days|Subject značí seskupování Subjektu po Dnech. Alternativou je zápis v podobě (Days - 1 | Subject)., kde jsou Dny také bez Interceptu.

Srovnání modelů fm8 a fm9:

Protože je Chisq (0,0639) velmi malý a „p-value“ velké (0,8004), nemůžeme zamítnout H0 ve prospěch alternativní hypotézy Ha, preferuje tedy model fm9. Toto tvrzení vyplývá i z předešlého Grafu 9., to znamená, že počáteční reakční doba nemá silný vztah na to, jak bude subjekt reagovat v průběhu spánkové studie s nedostatkem spánku.