Základní pojmy
Popis částí modelu modelu
Model GLMM se upevní na data DyestuffData z balíku lme4 pomocí funkce lmer a uloží se do proměnné fm1.
Dyestuff Data – obsahuje 30 vzorků (pozorování) a 2 proměnné a to Dávku (Batch) se 6 úrovněmi a Výnos (Yield) s 30 úrovněmi. Proměnná Výnos je odezva (vysvětlované, závislá proměnná) kovariátu (nezávislá, vysvětlující proměnná).
1. REML=TRUE
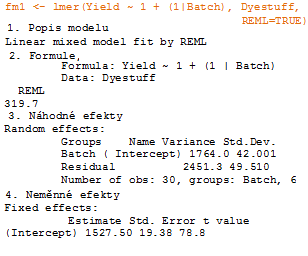
1. Popis modelu, zde je název použitého modelu, ve kterém jsou parametry odhadnuty s minimálním REML.
2. Formule a Data jsou zobrazeny jako zmínka, pro lepší orientaci ve výsledcích. REML, REML odhaduje variaci (odlišnost) komponentů (složek).
REML je zkráceně Restricted maximum likelihood a používá se k omezeným odhadům maximální pravděpodobnost. Používá pravděpodobnostní funkci spočítanou z transformovaného datasetu, tak že nevýznamné parametry nemají efekt. V takovém případě nejsou variační komponenty odhadnuty z originálního datasetu, ale ten je nahrazen sadou kontrastů vypočítaných z dat a pravděpodobnostní funkce.Ta je vypočítána z pravděpodobnostního rozdělení kontrastů. REML se velmi často užívá jako jedna z metod v uchycení lineárního mixovaného modelu. Pokud je RELM = FALSE, model je počítán pomocí maximální pravděpodobnosti MLE.
1. REML=FALSE
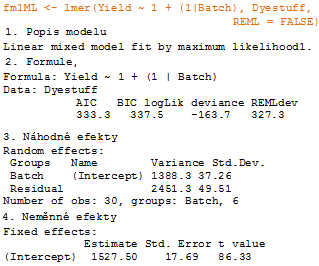
1. Popis modelu, zde je název použitého modelu, ve kterém jsou parametry odhadnuty pomocí maximální pravděpodobnosti.
2. Formula a Data jsou zobrazeny jako zmínka, pro lepší orientaci ve výsledcích.
AIC - Akaikeho informační kritérium (vhodnost modelu).
BIC - Schwarz-Bayesianovo informační kritérium (vhodnost modelu).
logLik – log-likelihood – logaritmická pravděpodobnost odhadovaných parametrů.
deviance – odchylka (dvakrát negativní log-likelihood) odhadovaných parametrů.
AIC, BIC, logLik a deviance jsou statistiky spojené s upevněním modelu a jsou použitelné ke srovnání různých modelů k uchycení stejných dat.
Maximum likelihood estimation - MLE, je metoda odhadu parametrů ve statistickém modelu. Tato metoda se používá, pokud není dostatečný počet měření. Hodnoty by měly mít Gaussovo (normální) rozdělení. Průměr a variance budou z MLE odhadnuty i z malého počtu měření. MLE v tomto případě vezme střední hodnotu a varianci jako parametry a hledá konkrétní parametrické hodnoty, které určí pozorované výsledky jako nejpravděpodobnější. Pro neměnná data a základní statistický model metoda vybírá hodnoty, které způsobují rozdělení dané pozorovanými daty s nejvyšší pravděpodobností (parametry maximalizují pravděpodobnostní funkci). MLE tedy podá jednotný odhad, který je nejlépe definovaný v daném případě s gaussovým (normálním) rozdělením a malým počtem základního měření.
3. Náhodné efekty, zde vidíme dva zdroje variability v upevněném modelu, a to variabilitu Dávky (Batch) k Dávce (Batch) v úrovni odezvy a Residual (pozůstatek) známý také jako variabilita pozorování nebo variabilita v rámci Dávky.
Residual je část variability, která nemůže být vysvětlena nebo modelována s ostatními výrazy. Je to změna či odchylka od pozorovaných dat, která zbyla po určení odhadů parametrů v dalších částech modelu. Část této variability je v odezvě asociována s výrazy neměnných efektů.
Intercept (průsečík), reprezentuje „typickou“ či střední úroveň odezvy v daném případě.
Standard deviation (směrodatná odchylka) je další odhad variability jako rozptyl. Směrodatná odchylka říká, jak moc se od sebe liší případy, které jsou typické ve zkoumaném souboru. Prvky jsou si tedy podobné, pokud je směrodatná odchylka malá a velká směrodatná odchylka vypovídá o velkých vzájemných odlišnostech. Také lze přibližně zjistit, jak daleko jsou hodnoty v našem souboru vzdáleny od průměru (střední hodnoty). Hodnota směrodatné odchylky je odmocnina variance (rozptylu).
Směrodatná odchylka se používá, poroto že se dá lépe prezentovat než variance (rozptyl). Směrodatná odchylka má měřítko odezvy avšak rozptyl má magnitudu.
Variance (rozptyl) popisuje variabilitu rozdělení pravděpodobnostní náhodné veličiny. Stejně jako směrodatná odchylka popisuje, jak si jsou hodnoty v souboru podobné.
Standard Error (střední chyba) je směrodatná odchylka výběrového rozdělení.
4. Neměnné efekty, zde jsou vytištěny odhady a směrodatné chyby pro všechny parametry neměnných efektů. Jediným neměnným efektem pro tento model je 1 z formule Yield ~ 1 + (1|Batch).
Modely s kříženými a vnořenými efekty
Efekty mohou být křížené, tzv. „crossed“, nebo mohou být vnořené, tzv. „nested“. Pro jednodušší pochopení se berou náhodné efekty jen jako „crossed“ či „nested“.
Modely s kříženými náhodnými efekty lze například využít u zjišťování reakcí lidí na dané podněty, protože každý jedinec vnímá stimuly jinak. Pokud je jedinec vnímán jako vzorek ze všech možných jedinců populace a stimuly jsou vzorkem z celé populace stimulů, pak je jen logické vnímat tyto dva faktory jako náhodné efekty. Stejně je to i u dotazníků, kdy každý jedinec odpovídá na otázky podle svého uvážení.
Pro takové výpočty se požívá balík lme4, který je schopen práce s rozsáhlými, nevyváženými daty s kříženými efekty a větším počtem seskupujících faktorů. To je pro reálné analýzy velmi užitečné. Zde však budou ukázány lehčí příklady pro pochopení.
Pokud jsou náhodné efekty spojovány s mnohonásobnými faktory, tak se použije stejná funkce pro výpočet modelu a nezáleží na tom, zda je faktor křížený nebo z části kříženy či zahnízděný. V případě, že se vyskytne „nested“ faktor pro slučovací faktory, je myšleno (1| faktor), tak je registrován, ale toto poznání nezmění postup výpočtu. Je možné použít diagnostiku, když se ví, že slučovací faktor je vnořený.
Modely s částečně kříženými náhodnými efekty
V reálném světě jsou běžné studie s mnoha seskupujícími faktory, které nejsou zcela vnořené nebo zcela křížené. Takové to studie označujeme jako studie s částečně kříženými seskupujícími faktory náhodných efektů. Příkladem může být studie, která zachycuje výsledky studentů za určitý čas. Studenti jsou spojováni s učiteli a školami. Pokud měli studenti v průběhu školní docházky různé učitele, nemůže být faktor studentů vnořený v rámci učitelů a také se kompletně nekříží faktor učitelů a studentů. Proto se pro tuto analýzu použije model s částečně kříženými náhodnými efekty.
Studie, která se zabývá analýzou různých faktorů za určitý časový interval, se nazývá longitudinální analýza. V tomto případě, longitudinální analýza zkoumá tisíce faktorů v podobě studentů a stovky faktorů v podobě učitelů za daný čas s náhodnými efekty, které jsou jen částečně křížené. Na nadcházejícím příkladu bude vysvětlena teorie. Ukázková studie ukáže, jak žáci ohodnotili své učitele.
Testování statistické hypotézy
H0:σ2=0 …nulová hypotéza
Ha:σ2>0… alternativní hypotéza
Chceme zjistit kvalitu umístění dvou modelů, které mají parametry σ2=0 a σ2>0. Tuto kvalitu zjistíme z tzv. „p-value“ (p-hodnota), cože je pravděpodobnost rozdílu v uchycení modelů. Hodnota p-value je v rozmezí od nuly do jedničky. Čím je hodnota p-value menší až blízká nule, tak mohu zamítnout nulovou hypotézu H0 ve prospěch alternativní hypotézy Ha a preferuji model Ha. Naopak pokud je hodnota p-value velká, tak nemohu zamítnout nulovou hypotézu H0 a preferuji model s H0.
Příklad:


Pro porovnání umístěných modelů fm3 a fm3a použije statistickou metodu s názvem anova, abychom zjistili, který model je lépe uchycen. Model fm3a zde přestavuje nulovou hypotézu H0 a model fm3 alternativní hypotézu Ha.

Protože je hodnota p-value velká, 0.5234, tak nemohu zamítnout nulovou hypotézu H0 a preferuji model s H0, tedy model fm3a. Abychom preferovali model fm3, tedy nulovou hypotézu, musela by být hodnota p-value menší než 0.05 či 0.01, podle toho zda počítáme s 5% chybou či jen s 1%.