Charakteristika variant

D8 (O'Callaghan a Mark, 1984) – SFD

Deterministic eight-nieghbors, zkráceně D8, je základní algoritmus typu SFD prezentovaný O’Callaghanem a Markem v roce 1984. Předností tohoto algoritmu je jednoduchost – každý pixel, který není sinkem, teče ve směru pouze a právě jednoho z osmi sousedů.

Směr odtoku je určen ve směru pixelu, v jehož směru je největší pozitivní změna nadmořské výšky (δZ). Hodnoty rozdílů nadmořských výšek sousedů v diagonálním směru jsou vynásobeny faktorem 1/√2 tak, aby byla kompenzována větší vzdálenost centroidů pixelů. Když takový pixel neexistuje, směr není definován. Je použito standardního kódování 2^d-1, kde směr odtoku d = 1, 2, …, 8, nebo 0 pro nedefinovaný směr. Nevýhodou algoritmu je výběr směru odtoku při rovnosti sousedů – je vybrán ten směr, který přijde na řadu jako první od severu ve směru hodinových ručiček (záleží na konkrétní implementaci).

Jenson a Domingue (1988) vyřešili tok přes ploché území iteračním procesem. Jejich postupem je nejdříve určen směr odtoku všech neplochých buněk. Následně v každé iteraci je přiřazen směr odtoku buňkám plochého území ve směru sousedních buněk, které už mají definován směr odtoku a které neodtékají ve směru testovaného pixelu. Tzn. že postupně narůstá počet buněk plochého území, které mají přiřazenu hodnotu FD, až do doby, kdy ji mají přiřazenu všechny buňky plochého území. Algoritmus tak rovněž elegantně řeší příslušnost plochých pixelů ke spill-pointům, kterých může být v jednom plochém území více.

Rho8 (Fairfield a Leymarie, 1991) – SFD

Svou prací se snažili posunout dále algoritmus D8, kterému vyčítali, že při orientaci pixelu např. v rozmezí od 22,5º do 67,5º bude výsledný směr odtoku přímý severovýchod. Tím chtěli poukázat na fakt, že algoritmus může vyhladit tvary v terénu, které mohou poukázat na konvergenci či divergenci toku. Snažili se vyřešit problém s tendencí tvořit paralelní toky, které nekorespondují s orientací svahu, a potlačit vliv umělých sinků. Také se zmínili o úskalí plynoucím z přílišné orientace na DMR založený na gridu při řešení flow routing problému a přiklánějí se (jako i jiní autoři) k vrstevnicovému modelu.

Metody, které prezentují ve své práci, se nazývají Rho4 (stochastic / random four-neighbors) a Rho8 (analogicky). Algoritmy se snaží zakomponovat myšlenku, že teoreticky očekávaná hodnota směru odtoku pixelu by měla být rovna orientaci pixelu, resp. roviny, která prokládá jeho nejbližší okolí. Tzn. např. nechť oblast má orientaci 15º východně od severu, řešením je, aby si dotčené pixely pravděpodobnostně vybraly orientaci S (0º) nebo SV (45º) tak, aby výsledný poměr přiřazených směrů odtoku byl 2:1 ve prospěch severní orientace.

Rho4 určí směr odtoku ve směru jednoho ze čtyř sousedních pixelů s největším gradientem – pro sousedy východozápadní (VZ) je gradient roven δZ, pro sousedy severojižní (SJ) je roven rho4 · δZ, kde rho4 je náhodná veličina nabývající hodnot (0; +∞).

Rho8 určí směr odtoku ve směru jednoho z osmi sousedních pixelů s největším gradientem – pro sousedy v ortogonálním směru je gradient roven δZ, pro sousedy v diagonálním směru je roven rho8 · δZ, kde rho8 je náhodná veličina nabývající hodnot (0,5; 1).

Na rozdíl od D8, který násobí hodnoty δZ v diagonálním směru faktorem 0,7071, algoritmus Rho8 násobí hodnoty δZ náhodnou veličinou, jejíž hodnoty mají průměr 0,7071. Sinky jsou zde brány jako skutečné, takže se nevyplňují, neupravuje se DMR, ale vyhledá se nejnižší bod sinku, ze kterého je pak nadefinován směr odtoku do dalších buněk.

Autoři se obhajují, že náhodná funkce nevnáší do dat šum, ale naopak dovoluje směru odtoku se lépe přiblížit ke skutečné orientaci svahu (oproti největšímu pozitivnímu sklonu vzhledem k jednomu sousedovi) a že nestabilita toku (změna jeho směru) je přírodním jevem. Tarboton (1997) kontruje, že náhodnost není žádoucí, protože upstream area a specific catchment area jsou veličiny jasně determinované a měli bychom být schopni je spočítat tak, aby byl výsledek vždy stejný. Při každém použití algoritmu Rho8 bude výsledek jiný.

MS (Quinn et al., 1991) – MFD

Jedná se o algoritmus z rodu MFD, který měl opět za cíl vyřešit omezení algoritmu D8. MS je zkratkou pro Multiple directions based on Slope (Tarboton, 1997). Tato metoda přiřazuje směr odtoku jednoduše všem nižším pixelům. Jednotkový objem odtoku mezi tyto pixely dělí poměrně podle sklonu k těmto pixelům – čím větší sklon, tím větší poměrná část. Existuje více obměn tohoto algoritmu (viz Freeman, 1991; Holmgren, 1994).

Tarboton (1997) považuje za nevýhodu, či dokonce nepřesnost, že je odtok z pixelu rozptýlen do všech nižších pixelů bez ohledu na jejich sousedství. Nepohlíží tak na pixel jako na jednotkový povrch (jak je tomu u následujících algoritmů Lea a DEMON), ale umožňuje ho dále dělit.

Tohoto algoritmu bylo využito při konstrukci MFD varianty dynamického modelu vývoje reliéfu.

Lea (Lea, 1992) – SFD

Tento algoritmus je zástupcem skupiny, která přiřazuje směr odtoku podle vektoru sklonu povrchu (hodnota orientace) v daném pixelu – jedná se o tzv. aspect-driven algoritmus = řízený orientací.

Povrch pixelu je aproximován rovinou „nasazenou“ na čtyři rohy analyzovaného pixelu – každému rohu je přiřazena nadmořská výška rovnající se aritmetickému průměru nadmořských výšek tří sousedních pixelů dotýkajících se dotčeného rohu. Lea (1992) vysvětluje tento postup pomocí balónku, který se koulí na jakékoli ukloněné ploše právě ve směru sklonu této plochy. Směr odtoku tak nabývá spojité hodnoty od 0 do 2p.

Variabilita algoritmu k obměnám je ve výpočtu sklonu a orientace pixelu – jedním přístupem je vypočítat spád k osmi (resp. čtyřem) sousedům a ve směru největšího spádu definovat i orientaci pixelu (zde však orientace nabývá pouze maximálně osmi hodnot); druhým a lepším přístupem je nasazení roviny na určité okolí analyzovaného pixelu. Povětšinou se uvažuje okno 3×3 pixely, ale lze použít i větší. Na z-tové hodnoty těchto pixelů se pak nasadí rovina, která má jasně analyticky definovanou orientaci i hodnotu gradientu. Ovšem i k nasazení roviny lze přistupovat různě.

Algoritmus patří do rodiny SFD – směr odtoku je určen do jednoho z osmi sousedů, avšak pravděpodobnost, že bude určen do diagonálních pixelů je malá, jelikož se s analyzovaným pixelem stýkají pouze v jediném bodě.

DEMON (Costa-Cabral a Burges, 1994) – MFD

Směr odtoku je stejně jako u předchozího algoritmu určen ve směru maximálního sklonu povrchu v daném pixelu. Hlavním přínosem je pohled na odtok z pixelu jako na plošný proces. Zdrojem odtoku je celá plocha pixelu, nejen jeho centroid, jak je tomu u ostatních algoritmů.

Lea (1992) použil k výpočtu sklonu tzv. block-centered grid, kde hodnoty elevací nesou centroidy pixelů. Costa-Cabral a Burges (1994) využívají k výpočtu maximálního sklonu tzv. edge-centered grid, kde elevace jsou zaneseny v průsečících linií gridu. Povrch pixelu je pak stejně aproximován rovinou nasazenou na čtyři body v rozích pixelu a z nich je vypočítán směr maximálního sklonu.

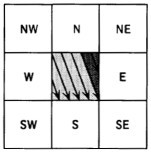
Pokud je směr odtoku násobkem 90º, všechen objem ze zdrojového pixelu jde do jediného sousedního pixelu. Pokud není násobkem 90º, objem odtoku je poměrně rozdělen mezi dva dotčené kardinální sousedy. Je zde vyloučen tok do diagonálních sousedů, protože kontakt s nimi se děje pouze přes bod. Aby tok dosáhl diagonálního souseda, musí projít přes souseda kardinálního.

Obrázek ukazuje, jak je tok rozdělen mezi jižního a východního souseda při úhlu odtoku 292º. Tmavší část vstoupí do pixelu východního a podíl z odtoku z centrálního pixelu se vypočte podle vzorce f_E = A_E / A, kde A_E je plocha tmavého trojúhelníku a A je plocha celého pixelu. Objem odtoku do jižního pixelu se pak vypočte ze vzorce f_S = 1 – f_E.

(převzato z Lea, 1992)

Zde je třeba uvést, že oba orientací řízené algoritmy DEMON i Lea nasazují rovinu při výpočtu orientace na čtyři body. Rovinu přesně definují tři body, které neleží v přímce. V těchto případech tedy vždy dochází k jakémusi vyrovnání roviny tak, aby co nejlépe kopírovala rozložení všech čtyř bodů. Tímto přístupem se stávají obě metody velice citlivé na extrémní hodnoty.

D∞ (Tarboton, 1997) – MFD

Po zhodnocení výhod a nevýhod předcházejících algoritmů přichází Tarboton (1997) s novým, vlastním. Jedná se o MFD algoritmus, který je do značné míry kompromisní a z předchozích si bere to, co Tarboton považuje za nejlepší. Přiklání se k použití algoritmu MFD, na druhou stranu ale poznamenává, že přílišná disperse odtoku z jednoho pixelu tak, jak ji aplikoval Quinn et al. (1991), je neslučitelná s definicí upstream area a specific catchment area a nabádá k minimalizaci disperse. Nový algoritmus sám označuje jako D∞ (resp. D-inf, D-infinity) ve smyslu nekonečného množství možných jednoduchých směrů odtoku.

Tarboton tedy prezentuje svou metodu jako SFD, determinovanou směrem nejstrmějšího sklonu (spojitá hodnota mezi 0 a 2p), který je počítán z osmi trojúhelníkových plošek uspořádaných v okně 3×3 pixely se zájmovým pixelem uprostřed. Použitím těchto plošek se algoritmus vyhýbá aproximaci (ve smyslu zvýšení nepřesnosti) při nasazování roviny na čtyři body v případě algoritmu DEMON, protože nasazuje rovinu na tři body, které přímo definují onu rovinu. Tam, kde vypočítaný směr nejstrmějšího sklonu nesleduje přímo jeden z ortogonálních (0, p/2, p, 3p/2) nebo diagonálních (p/4, 3p/4, 5p/4, 7p/4) směrů, je jednotkový objem odtoku rozdělen poměrně mezi dva sousední nižší pixely podle toho, jak se směry odtoku přimykají k vektoru nejstrmějšího sklonu. Tzn. že odtok je rozptýlen (MFD), ale vždy maximálně do dvou směrů.

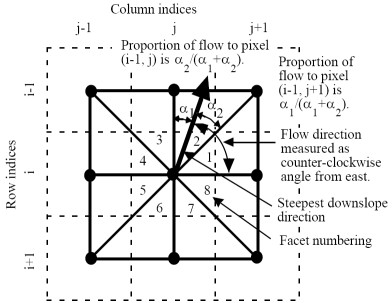
(převzato z Tarboton, 1997)

Předpokládejme teď, že centrální pixel je vrcholem a všechny okolní pixely jsou nižší. Každá z plošek (resp. rovin) pak bude mít downslope vektor, který pokud jej vykreslíme z centroidu centrálního pixelu, bude ležet uvnitř nebo mimo analyzovanou plošku, mimo 45º výseč. Pokud bude vektor ležet uvnitř plošky, reprezentuje nejstrmější směr odtoku v rámci této plošky. Pokud bude ležet mimo danou plošku, nejstrmější směr odtoku bude definován podél okraje plošky (který tak představuje nejstrmější část plošky). Směr nejstrmějšího sklonu pro centrální pixel je pak ztotožněn s nejstrmějším downslope vektorem jedné z osmi plošek.

V případě, že má více plošek stejný sklon, za nejstrmější sklon je vybrán první z nich, který přijde na řadu v pořadí plošek od 1 do 8. V případě, že žádný sklon není pozitivní (jedná se o plochou buňku), je pro flow direction použita hodnota -1, která signalizuje, že FD pixelu není vyřešeno. Tok přes tyto pixely je pak vyřešen SFD metodou Jensona a Dominguea (1988).